Tehnology
DAS Technology
In the following section we are giving a brief outline, which we try to make suitable also for the non-expert reader, about the technology and physical principles underlying the SLAM-DAST project sensor system, which is based on both stimulated Brillouin scattering effects as well as Rayleigh scattering along single-mode optical fibers, and exploits two techniques in the interrogating equipment for strain and acoustic sensing respectively: Brillouin optical time-domain analyisis (BOTDA) and phase optical time domain reflectometry (φ-OTDR).

Distributed Acoustic Sensing (DAS), also knows as Distributed Fiber Optic Sensing (DFOS), is an emerging type of distributed sensing technology that uses lasers to sense sound in real time along an optical fiber cable. Simply by plugging into one end of a normal optical fiber cable, a DAS unit causes the fiber to behave like 1000s of vibration sensors, or microphones, spread out over many kilometres, with no additional electronics or hardware. The distributed Brillouin sensing technique has been developed rapidly since its first demonstration three decades ago. Numerous investigations on the performance enhancement of Brillouin sensors in respect to spatial resolution, sensing range, and measurement time have paved the way to its industrial and commercial applications. Since optical fibers can be used to measure a variety of physical parameters directly or indirectly, sensing in optical fibers has been intensively investigated in the past few decades. Fiber optic sensors can be split into two big categories, that is, point and distributed sensors. The former type, such as the fiber Bragg grating (FBG), measures the physical parameters only at a particular location but with relative high resolution and sensitivity. The detectable range of the latter one, such as optical time-domain reflectometry (OTDR), is relatively large (usually the fiber length itself) and continuous but with only moderate resolution and limited sensitivity. However, numerous investigations have been carried out to design a novel sensor with the advantages of both types, but avoiding their disadvantages. With a moderate spatial resolution in the range of 1 m, distributed Brillouin sensing offers a more cost-effective solution than applying numerous point sensors in long-range sensing and a more accurate result than traditional distributed sensing methods such as OTDR. Due to the recent success in breaking the limits of numerous sensing parameters such as spatial resolution, sensing range, and measurement time, the Brillouin sensing technique has proved its eligibility in a variety of fields. Thus, it has aroused significant interest in many different applications like civil engineering, oil and gas pipelines leakage monitoring, and other infrastructure surveillance tasks.
According to the DES of SBS, the Brillouin gain in each fiber section is accumulated in an SBS interaction between two continuous waves (CW). This accumulation along the fiber leads to a relative high energy conversion at the detector but makes it difficult to distinguish the information of local interactions. Therefore, distributed Brillouin sensing uses other techniques.
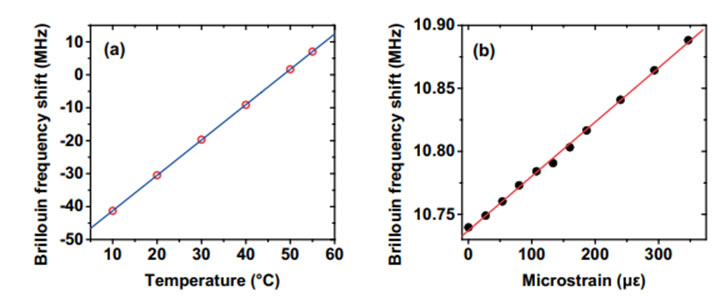
According to the theory of material science, the velocity of the longitudinal acoustic mode in the fiber depends on material properties such as Young’s moduli and the density. This high sensitivity to the temperature and tensile strain makes the BFS also temperature and strain dependent. The linear dependence has been proved and measured in several papers, as illustrated in Figure.
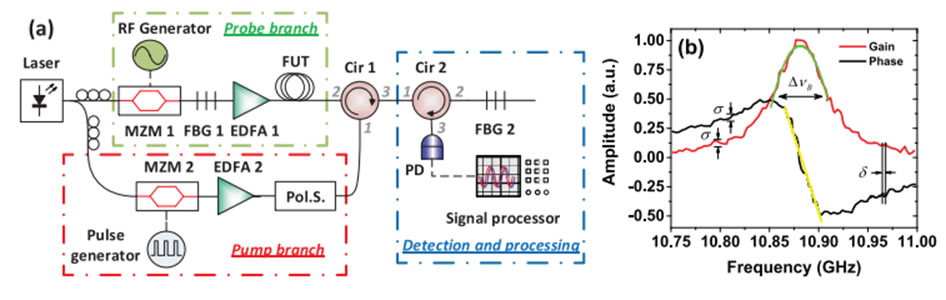
As illustrated in Figure, a typical conventional BOTDA setup mainly comprises three parts. A highly coherent laser is split via a coupler into the probe (upper) and pump (lower) branch. A microwave signal, which can be scanned over the range of the BFS (11 GHz – 150 MHz), is applied on a Mach-Zehnder modulator (MZM 1) in the probe branch and biased in the carrier suppression regime. The generated lower frequency sideband serves as the probe wave, while the upper one is blocked by a narrow band-pass filter (FBG 1). The probe power is controlled by an erbium-doped fiber amplifier (EDFA 1) and launched into one end of the FUT. In the pump branch, the pump pulse with a required duration is formed by another MZM, amplified by EDFA 2 and launched into the other end of the fiber via a circulator (Cir 1). In order to mitigate the influence of the SBS polarization effect, the polarization of either pump or probe wave is scrambled via a polarization scrambler (Pol.S.) before launched into the fiber. The Brillouin amplified probe wave is detected by a fast photodiode (PD) whose minimum bandwidth should correspond to the inverse of the pump pulse duration, to avoid any trace distortions. Another narrow band-pass filter (FBG 2) blocks the residual reflected pump wave. The electrical signal from the PD, which represents the evolution of probe power, is processed digitally with a large number of averaging by a signal processor, that is, an oscilloscope or a digitizer. The Brillouin gain, which is essential for BFS estimation, can be derived by dividing the output of the PD by the probe power before the pump pulse is launched into the fiber.
The enhanced SNR and the moderate resolution are the superiority of distributed Brillouin sensors to the traditional distributed and point sensors in long-range sensing. However, conventional BOTDA sensors are limited by MI and NLE. The origins, as well as methods for the mitigation of MI and NLE, have been presented and discussed in detail. Thus, with these new methods, much longer sensing ranges became possible. Besides the sensing range, methods to enhance the spatial resolution and the speed of the measurement have also been reviewed and discussed. Nowadays, distributed Brillouin fiber sensors can have a resolution in the centimeter range, or even below and act like thousands or millions of point sensors. At the same time, novel ideas such as multi-tone pumps have successfully shortened the measurement time in distributed SBS sensors from several minutes down to 10 ms. Due to the fruitful proof-of-concept results, some of the state-of-the-art techniques discussed in this chapter have already been applied in some BOTDA prototypes.
Fiber-optic-based distributed acoustic sensors (DASs) have been under extensive investigation in the last years due to their capability of providing measurements of thousands of distinct sensing points along sensing fibers, which are immune to electromagnetic interference and can be easily reinforced for harsh environmental conditions. Because of this, they have seen a rising demand in fields such as civil engineering, oil and gas industry, security, and geophysics, for applications such as pipeline leakage monitoring, engine vibration control, structural crack detection, or human intrusion monitoring. In particular, phase sensitive optical time domain reflectometry (ϕ-OTDR) has proven to be one of the most effective DAS approaches, due to its capability of acquiring quantitative dynamic strain variations of frequencies up to a few kHz simultaneously and in real time over tens of kms of sensing fiber, thus overcoming the typical limitation of Raman- or Brillouin based fiber sensors. One of the phase demodulation methods developed in recent years involves the use of Mach– Zehnder or Michelson 3×3 interferometers to perform the phase calculation at different points of the fiber directly in the optical domain. This type of design has been successfully employed for a variety of applications, such as monitoring of submarine cables and railways. In any application, the elimination of noise sources to obtain acceptable levels of signal-to-noise ratio (SNR) for phase demodulation is a crucial aspect. In fields such as intruder detection, for example, noise reduction over the entire spectrum becomes relevant not only for measurement accuracy, but also for improving the performance of machine learning methods employed to classify different events. Different approaches have been developed for this goal, mainly at the postprocessing level, by employing different noise elimination techniques, such as moving averages, differential phase methods, continuous wavelet transforms, time signal separation algorithms, or adaptive two-dimensional bilateral filtering. While these methods are effective, their algorithmic nature means their implementation comes at a cost in terms of processing speed requirements of the sensing system; thus, there is a trade-off between noise suppression and either frequency range or required processing power in real time applications.

www.dastsensing.net
